Il cerchio di centro (0,0) e raggio 1. La parte superiore è il grafico di F: x → √(1-x²)

Quanto è lungo l'arco di cerchio che va da (1,0) al punto P di ascissa -0.8?

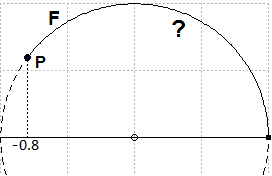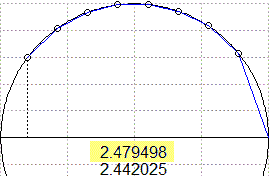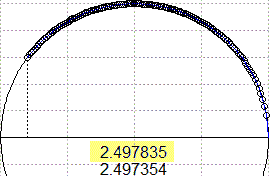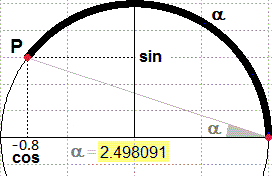
Lo approssimo con un segmento di cui calcolo la lunghezza col teorema di Pitagora. Poi, diviso [-0.8,1] in 2 parti uguali, l'approssimo con la somma di 2 segmenti di cui calcolo la lunghezza con lo stesso teorema. E così via. Ottengo una successione di valori che tende alla misura esatta. Arrotondata a 7 cifre è 2.498091. Se invece di -0.8 considerassi -1 otterrei 3.141593, l'arrorondamento di π. La lunghezza dell'arco viene considerata la misura dell'angolo α. Ordinata e ascissa di P sono invece chiamate seno e coseno di α.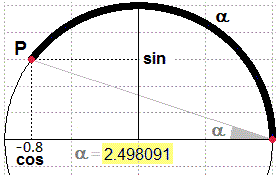

In maniera simile si può trovare la lunghezza di archi di altre curve,
approssimandoli con un numero via via maggiore di segmenti.